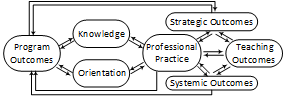
Development of the challenge space is ongoing and includes input from classroom mentor teachers, mathematics coaches and supervisors, and teacher candidates and program completers. The goals of the program are viewed through four constructs: teacher knowledge, teacher orientation (e.g., attitudes, beliefs, self-efficacy), teacher practice, and student outcomes. Teacher knowledge and orientation influence each other and inform teacher practice. Teacher practice includes reflection on student outcomes, thereby reinforcing or refining teacher knowledge and orientation and informing the program (i.e., feedback loop).
Vision
The mathematics teacher preparation program is designed to help candidates explore, enact, and insist upon equitable teaching practices to support robust mathematics learning communities. Learning communities are defined as collaborative groups that are pursuing common goals for mathematics learning experiences. Learning communities that are safe, humanizing, collaborative, and culturally-aware empower participants to direct their engagement in scientific inquiry and the examination of diverse ideas and perspectives. Candidates enter the field ready to improve the quality of mathematics teaching and learning for each and every student in their classrooms, schools, and districts and to become societal change agents in the field.
Standards
Ecojustice, Social Justice Framework Standards, InTasc Standards, Common Core Standards for Mathematics, NCTM process standards, NCTM Effective Teaching Practices, NCTM CAEP standards, NCTM Catalyzing Change, AMTE Teacher Preparation Standards
Goals
Teacher Knowledge
- Subject Matter Knowledge. Teachers have robust knowledge of mathematics, understanding how concepts and procedures are inter-related, and how to frame mathematics knowledge in a meaningful way to help students learn (Mathematics Knowledge for Teaching).
- Pedagogical Content Knowledge. Teachers develop robust pedagogical knowledge to support deep mathematics learning in their classrooms, including the use of tools for teaching mathematics (Knowledge for Teaching Mathematics).
- Knowledge of Orientation. Teachers understand and respect the relevance of the affect of each member of a learning community (e.g., attitudes, culture, beliefs, values, confidence, anxiety) in learning mathematics.
- Knowledge of Discernment. Teachers understand that discernment encompasses the connections between cognition, metacognition, and learning and decision-making processes. Knowledge of discernment includes understanding developmental processes and the socio-emotional and sociocultural components of learning.
- Knowledge of Individual Context. Teachers understand that learning and decision-making processes take place within the context of the intersectionality of social categories.
- Knowledge of Environmental Context. Teachers understand the importance of building an inclusive and equitable environment to support a robust learning community.
Teacher Orientation
Orientation plays an important role in how teachers approach the profession individually as well as in collaboration with students, colleagues, schools and community. Orientation includes but is not limited to constructs such as attitudes, perceptions, self-efficacy, beliefs, confidence, self-concept, motivation, value of mathematics, interest in mathematics, enjoyment of mathematics, enjoyment of teaching, usefulness of mathematics, mathematics goals, professional goals, attributions of success/failure, mathematics anxiety, professional anxiety, professional dispositions, commitment to lifelong learning, perceptions of power and agency.
These orientations can be about a wide range of topics, including but not limited to mathematics, teaching and learning, assessment, students, socio-cultures, families and caregivers, collaboration, the profession, a school or district.
Teachers examine orientation as an ongoing part of their growth and learning to ensure that all aspects of the profession are approached through a productive lens. Teachers are willing to change their views when appropriate.
Teacher Practice
- Culture. Teachers establish a culture of access and equity through classroom structures and culturally relevant pedagogy to support each and every student in learning and participating in mathematics deeply. These classroom structures empower students to value diverse perspectives by elevating their voices , providing leadership opportunities, and developing a strong learning community. Teachers model vulnerability, viewing mistakes as learning opportunities. Varied approaches are visible and valued.
- Active Engagement. Teachers actively engage students in learning mathematics and/or science with meaning.
- Conceptual Understanding. Teachers explicitly foster, model, and insist upon conceptual understanding and coherence for all learners at all levels as a primary means for promoting procedural understanding in mathematics. Teachers insist that all teaching activities and learning experiences embrace the development of conceptual understanding as the fundamental core of learning and form the foundation for peer discussions.
- Connections. Teachers structure lessons through an inquiry approach, recognizing that authentic contexts are the foundation of the lesson and frame the content to be learned. Contexts are not simply enrichment that happens after the “real” lesson if at all.
- Reasoning. Inquiry-based projects are incorporated in every unit. Quantitative reasoning is modeled as scientific inquiry (claim, evidence, rationale).
- Questioning. Questioning is purposefully crafted to foster higher order thinking and alternative modes of thinking about mathematics. Teachers pose questions of their students and encourage their students to ask deep, rich questions about their mathematical reasoning and that of their peers.
- Assessment. The ability to provide students feedback through formative (ongoing) and summative (reflective) assessment is differentiated from and valued more than grades. Assessments are ongoing, aligned to standards and (in)form teacher practice. Teachers understand that assessment can take many forms including formative (ongoing) and summative (reflective) assessment. Teachers incorporate a variety of assessments to ensure that each and every student has an opportunity to express their current understanding, including but not limited to observations, student-to-student and student-to-teacher dialogue, projects, performance tasks, interviews, portfolios, presentations, exit slips, dynamic technology-based activities. Teachers recognize that understanding develops over time and leverage opportunities to reassess throughout the learning process.
Student Outcomes
Teachers assess and reflect upon a wide range of student outcomes to inform their practice such as social and emotional well-being, persistence, goal setting, achievement, thinking/reasoning/explaining, orientation, cognition and meta-cognition, and learning behaviors.
Outcome Measures (Targets)
Target of 3.20 on all rubrics or score of “Proficient” on qualitative-only rubrics.
Teacher Knowledge
- Subject Matter Knowledge. Praxis II Content Exam, Content Expertise Project, mathematics course GPA (3.0 or better), Student Teaching Assessment Record (STAR) Standard 4.
- Pedagogical Knowledge. Praxis II PLT 7-12 Exam.
- Pedagogical Content Knowledge. STAR Standards 1, 2, 5, 6, 7, and 8. NCTM Student Teaching Evaluation Rubric, Reformed Teaching Observation Protocol (RTOP), EdTPA portfolio tasks, philosophy of teaching mathematics.
- Knowledge of Discernment. STAR Standards 1, 2, and 9. Student Learning Objective Project Experience (SLOPE)
- Knowledge of Orientation. STAR Standard 9.
- Knowledge of Individual. STAR Standards 1, 2, 10.
- Knowledge of Environment. STAR Standard 3.
Teacher Orientation
- NCTM Teaching & Learning Beliefs Survey
- NCTM Assessment Beliefs Survey
- Bandura’s Teacher Self-Efficacy Scale
- Secondary Program Dispositions Survey
Teacher Practice
- STAR
- RTOP-E
- NCTM Student Teaching Evaluation Rubric
- Phase I to Phase II Transition Performance Assessment
- EdTPA Portfolio
- Student Learning Objective Project Experience (SLOPE)
Student Outcomes
- SLOPE